astronomy notes - radius of curvature

1. Newtonian Telescope Notes by Dr. Eric Hooper
2. Radius of Curvature Notes by Dr. Eric Hooper
3. Optics Notes by Dr. Eric Hooper

Consider a spherical mirror of radius R. By definition, the radius intersects the sphere as a perpendicular. A schematic of the cross section is to the left. Our goal is to figure out focal length.

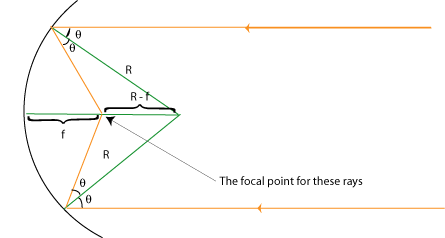
Now consider parallel light rays coming from a distant source. For simplicity, we'll only look at two rays, equidistant from the center point of the mirror. Each ray strikes the mirror at an angle with respect to the radius. Since the radius is the normal, the ray reflects on the other side at the same angle, , because of the fundamental law of reflection.

f is the focal length.

Nest we need to draw some lines and define a couple of new quantities, in order to relate f, R, and .

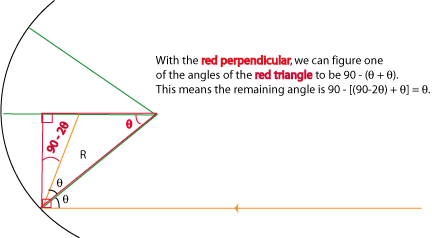
Now we know we have an isosceles triangle. If we drop a perpendicular, it bisects the long side into two segments, each R/2 long. This triangle is outlined in red.

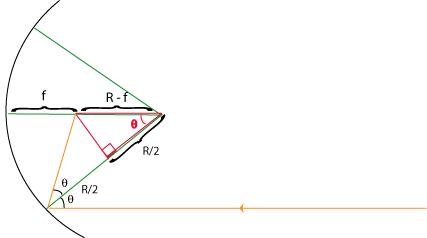
Looking at the red triangle, we have a simple trig relation:

After a little algebra,	(R - f)cos = R/2
	R - f = R / 2 cos
Divide both sides by R,	1 - f/R = 1/ 2cos

Finally, We have the focal length in terms of R and .
This means that all rays with the same focus at the same point. Rays with a different focus at a slightly different point. This is spherical abberation. As an approximation for small , cos1=> f/R1 - 1/2 => f R/2.

home    |    field activities   |    semester project    |    course information