Name: Daniel FitzPatrick
Title of Lesson: Pythagorean Theorem and Baseball
Date of Lesson: Day 13 (Wednesday)
Overview: To explore and make connections between the Pythagorean Theorem, the real world, and other areas of mathematics.
Performance Objectives:
The students will be able to:
-recognize, use, and learn about mathematics in contexts outside of mathematics
-use the Pythagorean Theorem to solve problems
TEKS:
3) The student understands how algebra can be used to express generalizations and recognizes and uses the power of symbols to represent situations.
(A) The student uses symbols to represent unknowns and variables.
(B) Given situations, the student looks for patterns and represents generalizations algebraically.
4) The student understands the importance of the skills required to manipulate symbols in order to solve problems and uses the necessary algebraic skills required to simplify algebraic expressions and solve equations and inequalities in problem situations. Following are performance descriptions.
(A) The student finds specific function values, simplifies polynomial expressions, transforms and solves equations, and factors as necessary in problem situations.
(B) The student uses the commutative, associative, and distributive properties to simplify algebraic expressions.
Materials:
· a. paper and pencil
· b. graphing calculator
· c. handouts of group activity questions
Activity
|
Teacher Does |
Student Does |
Ongoing Evaluation |
| Give a brief review of right triangles and the Pythagorean Theorem. |
Students listen and take notes. |
|
|
Engage: “Did you know that one of our Presidents of the United States of America gave a proof for the Pythagorean Theorem?”
Ask questions to engage students about the lesson. (See ongoing evaluation) |
Students answer questions and discuss their thoughts as a class. |
Do we really ever use the Pythagorean Theorem? Can we think examples where we would? How could the Pythagorean Theorem be used in baseball? |
|
Explore: Have students work on the activity “Baseball and the Pythagorean Theorem” (attached below). |
Students work on the activity. |
How was the Pythagorean Theorem useful in this baseball problem? Are there any other methods you can use to solve this problem? |
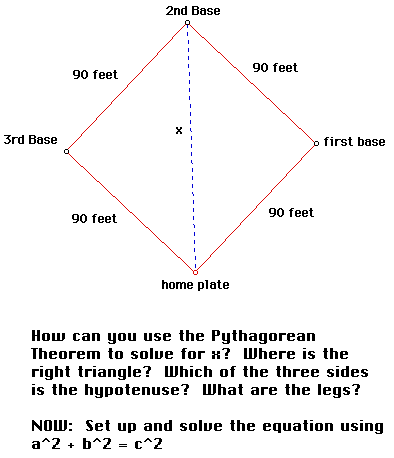
Baseball and the Pythagorean Theorem

The baseball "diamond" is really a square! We can use the Pythagorean Theorem to answer a question about this baseball Square.
(Photograph taken by Eddie Keel at the July 11th Minnesota-Cleveland Game at the HHH Metrodome. Used with permission.)

|
Explain: The Pythagorean Theorem is applicable in situations where right triangles exist. The Theorem states, given a right triangle with sides a, b, and hypotenuse c, then the length of the hypotenuse can be found by c2=a2+b2. |
Students listen to explanation. |
Is the converse of this statement true? |
|
Extend/Ellaborate: Have students work on the activity entitled “The Distance Formula revisited” (attached below) |
Students work on the activity. |
Do you see the connection between the distance formula and the Pythagorean Theorem? Can you think of a baseball situation where this might be used? |
The Distance Formula Revisited:
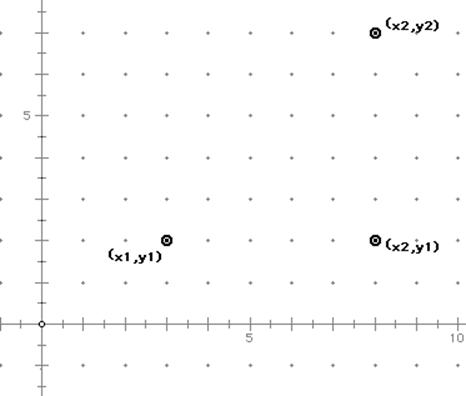
We've already seen and practiced the distance formula. Now, let's see if we can use the Pythagorean Theorem to understand why it works.
What should we try first?
(Hopefully, the students will suggest finding the distance between each of the points.--Think of them in terms of a triangle.)
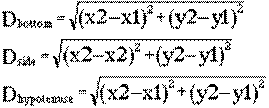
Now, what?
(Maybe they'll try putting these distances into the Pythagorean Theorem.)
![]()
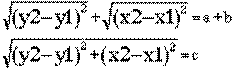
So, by squaring both sides we get...
![]()
------------------------------------------------------------------------------------------------------------
|
Evalulate: Ask a students to state the Pythagorean Theorem and give examples of how it might be used in regards to baseball problems.
Ask students to describe the connections between the distance formula and the Pythagorean Theorem. |
Students answer questions. |
Do you see the connection between the distance formula and the Pythagorean Theorem? Can you think of a baseball situation where this might be used? |
Lesson ideas used from the following websites:
http://jwilson.coe.uga.edu/EMT668/EMAT6680.F99/Challen/pythagorean/lesson4/lesson4.html
http://www.geom.uiuc.edu/~demo5337/Group3/bball.html