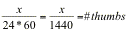LESSON PLAN

Name: Katherine Brown

Title of lesson: Sun Lesson

Date of lesson: March 23, 2005 and March 30, 2005

Length of lesson: 90 minutes

Description of the class: Math Class

Name of course: Algebra I

Grade level: High School

Honors or regular: Unknown

Source of the lesson:

Collaboration of professor and websites:

http://www.windows.ucar.edu/tour/link=/kids_space/distance.html

http://neo.jpl.nasa.gov/glossary/au.html

TEKS addressed:

(1) The student understands that a function represents a dependence of one quantity on another and can be described in a variety of ways. Following are performance descriptions.

(B) The student gathers and records data, or uses data sets, to determine functional (systematic) relationships between quantities.

(D) The student represents relationships among quantities using concrete models, tables, graphs, diagrams, verbal descriptions, equations, and inequalities.

(3) The student understands how algebra can be used to express generalizations and recognizes and uses the power of symbols to represent situations. Following are performance descriptions.

(A) The student uses symbols to represent unknowns and variables.

(B) Given situations, the student looks for patterns and represents generalizations algebraically.

I. I. Overview

The purpose of this lesson is to give students an understanding the concept of and the application of ratios and proportions. This is important in understanding how to correctly use telescopes.

II. Performance or learner outcomes

Students will be able to calculate the diameter of the sun.

Students will be able to explain how they calculated the diameter of the sun using ratios.

III. Resources, materials and supplies needed

4 telescopes

17 whiteboards, four for each telescope and one for teacher

Markers for whiteboards

Paper towels to wipe off whiteboards

Model of sun and earth 

Paper to cover telescopes

Pen to poke holes

Tape 

IV. Supplementary materials, handouts.

Five-E Organization

Teacher Does Probing Questions Student Does

Engage: Learning Experience(s)  Discussion of characteristics of the sun. The sun is an astronomical unit away from earth, which is 149,598,870,000 meters or 149, 598, 870 kilometers. The sun’s temperature is 5500 degrees Celsius and 9932 degrees Fahrenheit. The sun spots are 4000 degrees Celsius. The moon is 384,400 km from the earth. The moon’s temperature is 107 degrees Celsius during the day and -153 degrees Celsius at night. So today when we are outside, nobody is to look in the telescope while they are pointed to the sun. This will fry your eyes and you will no longer be able to see. I will appoint four students to each be responsible for monitoring the telescopes and preventing any injuries. Now lets go outside.

Critical questions that will establish prior knowledge and create a need to know Does anyone know what an astronomical unit is? Does anyone know exactly how far away the sun is? How hot do you think the sun is? In contrast to the sun, what do you think about the moon? How far away is the moon from earth? What about the temperatures of the moon? Where does the moon get its light? Does the moon spin on its axis like the earth does on a daily basis? So from your last lesson, who can explain the field of view and the ratios you used? Okay, now we will be using that knowledge to try and determine the diameter of the sun. Has anyone ever told you not to look directly at the sun?? Has anyone ever used a magnifying glass to burn and kill ants before? Why did that happen? Knowing this, what do you think would happen if you looked at the sun through a magnifying glass? What is a telescope?

Expected Student Responses/Misconceptions Many possibilities, but “The distance from the earth to the sun.” Many guesses. Many answers. Many guesses. The moon gets its light from the sun, just like earth. Hotter during the day, but cold at night. The moon doesn’t rotate on its axis. In our last lesson, we noticed we could see 40 cm through the telescope set 24 meters away. So we set up a ratio of 40 cm to 2400 cm, which turned out to be 1/60. Then if we had a ball that took up about half of that field of view at the 24 meter mark, then we knew that the ball was 20 cm in diameter, since ½ of 40 is 20, or we could set up the equation: 1/60 = (2x)/2400 and solve for x. Yes, this is to protect our eyes. Yes. That happened because the magnifying glass intensifies the sun’s rays and made it so hot that the ants burned up. Your eyes would burn up. A really big magnifying glass.

Explore: Learning Experience(s) Have the students assigned to monitor the telescopes be placed in the correct position. Place the paper over the telescope. Poke holes in the paper. Have the students aim the telescopes so that the light from the sun is no longer visible on the paper. Instruct the students to then back away from the eyepiece and use the whiteboard to see if they can see an image. Instruct them to use the markers to draw the image projected onto the whiteboard. Now, have the students hold the whiteboard steady and have the other students gently rock the telescopes in order to see where the sun escapes the field of view. Have the students mark the arcs created and form a circle.

Critical questions that will allow you to decide whether students understand or are able to carry out the assigned task (formative) Why would we want to cover the telescopes with paper? What do you see? What do we need to do next in order to determine the size of the sun? Any ideas how we might do that without looking into the telescope? What if we move the telescope around like this? Where is the sun going? Why is there just a portion visible on the whiteboard now?

Expected Student Responses/Misconceptions Because the light would be too bright from the sun to create a clear vision of the sun. The sun’s image. We need to determine how much of the field of view the sun takes up. Oh, the sun is going out of the field of view, so where it is no longer visible, we know that that is the field of view.

Explain: Learning Experience(s) Okay, so the sun is 149,598,870,000 meters away from the earth. That is 14,959,887,000,000 cm. The actual diameter of the sun is 1.392,000 km. So now let’s go back and measure the model of the sun and see how accurate the model is. Repeat activity, but now with students looking at the yellow ball through the telescope and determining the diameter of the model.

Critical questions that will allow you to help students clarify their understanding and introduce information related to concepts to be learned  Now what portion of the field of view did the sun take up? What can we do now to find the diameter of the sun? How will we set up the equation? Is this a good approximation?? How could we have gotten a closer answer? So what are the differences in the measurements? Why do they come out this way?

Expected Student Responses/Misconceptions It took up about half of the field of view. If you give us the distance to the sun, then we can find the diameter using our ratio of 1/60. This is good. We are approximating the amount of space the sun takes up in the field of view. If we had a better way to measure this, we could be more accurate.

Extend / Elaborate: Learning Experience(s)  So now we have the diameter of the sun. Discuss solar eclipses and how the moon and the sun appear to be the same size from earth. There are lunar eclipses rather often, the next one will be April 24^th. But the solar eclipses are much more rare. The last one was August 11, 1999. If you multiply that by 4, then you will have the number of thumbs in a full circle. Determine the time: Okay, we will use the telescopes again, make sure that you are not looking in the eyepiece. Find your field of view and have the sun line up right next to the edge. Then after the sun disappears from the field of view, then we know that it has moved its diameter’s distance. Make sure not to touch the telescope, however the whiteboard may be moved. Try to look at the moon tonight at different times. Look at it on the horizon and up in the sky. Use your thumb and determine how many thumbs wide it is.

Critical questions that will allow you to decide whether students can extend conceptual connections in new situations How long do you think it will take the sun to move its diameter in the sky? Think about the moon, it appears to be the same size as the sun in the sky. How many of your thumbs would it take to cover up the moon? Now how many thumbs do you have in a 90 degree angle? How long should it take your thumb (sun) to go around in a full circle? So how long will it take for your sun to move its diameter in the sky? How long did it take? So if our time is so different where did the error occur?

Expected Student Responses/Misconceptions The students approximate 1-5 thumbs. 24 hours. Maybe about 7 to 10 minutes. Only 2 to 3 minutes. The error happened when we said the sun was 5 thumbs wide. I guess it is only 1 thumb wide.

Evaluate: Lesson Objective(s) Learned (WRAP ≠UP at end) -> Summarize

Critical questions that will allow you to decide whether students understood main lesson objectives So what did you learn today? How did we use ratio and proportion?

Expected Student Responses/Misconceptions Lots of cool stuff. We used it with the sun’s diameter, with the model’s diameter, with the thumb and the timing of the sun’s movement.