TEMPLATE FOR LESSON PLANNING

PBI Telescope Preparation (2)

LESSON PLAN # __2_____ ClassDay/Time__________

Technology Lesson? Yes )

Name(s): Lauren Siegel

Title of lesson: Parabolas/ Reflection Geometer Sketchpad exploration

Date of lesson:

Length of lesson: 45 minutes

Description of the class:

Name of course: Algebra II

Grade level: 11

Honors or regular: Regular

Source of the lesson:

Dr. Eric Hooper's Astronomy prep lectures.

Sullivan, Michael, Precalculus Prentice Hall Chapter 9 p. 668.

Diagrams made in Geometer Sketchpad.

TEKS addressed:

Give identification number and letter and write out the TEKS.

a) Basic understandings.

(3) Functions, equations, and their relationship. The study of functions, equations, and their relationship is central to all of mathematics. Students perceive functions and equations as means for analyzing and understanding a broad variety of relationships and as a useful tool for expressing generalizations.

(4) Relationship between algebra and geometry. Equations and functions are algebraic tools that can be used to represent geometric curves and figures; similarly, geometric figures can illustrate algebraic relationships. Students perceive the connections between algebra and geometry and use the tools of one to help solve problems in the other.

(5) Tools for algebraic thinking. Techniques for working with functions and equations are essential in understanding underlying relationships. Students use a variety of representations (concrete, numerical, algorithmic, graphical), tools, and technology, including, but not limited to, powerful and accessible hand-held calculators and computers with graphing capabilities and model mathematical situations to solve meaningful problems.

(6) Underlying mathematical processes. Many processes underlie all content areas in mathematics. As they do mathematics, students continually use problem-solving, computation in problem-solving contexts, language and communication, connections within and outside mathematics, and reasoning, as well as multiple representations, applications and modeling, and justification and proof.

(b) Foundations for functions: knowledge and skills and performance descriptions.

(1) The student uses properties and attributes of functions and applies functions to problem situations. Following are performance descriptions.

(A) For a variety of situations, the student identifies the mathematical domains and ranges and determines reasonable domain and range values for given situations.

(B) In solving problems, the student collects data and records results, organizes the data, makes scatterplots, fits the curves to the appropriate parent function, interprets the results, and proceeds to model, predict, and make decisions and critical judgments.

(1) The student connects algebraic and geometric representations of functions. Following are performance descriptions.

(A) The student identifies and sketches graphs of parent functions, including linear (y = x), quadratic (y = x²), square root (y = Ö x), inverse (y = 1/x), exponential (y = a^x), and logarithmic (y = log_ax) functions.

(B) The student extends parent functions with parameters such as m in y = mx and describes parameter changes on the graph of parent functions.

(2) The student knows the relationship between the geometric and algebraic descriptions of conic sections. Following are performance descriptions.

(B) In order to sketch graphs of conic sections, the student relates simple parameter changes in the equation to corresponding changes in the graph.

(2) The student interprets and describes the effects of changes in the parameters of quadratic functions in applied and mathematical situations. Following are performance descriptions.

(B) The student uses the parent function to investigate, describe, and predict the effects of changes in a, h, and k on the graphs of y = a(x - h)² + k form of a function in applied and purely mathematical situations.

I. Overview

This lesson will give students an opportunity to explore parabolas and circles, in terms of reflection and location of the focus in particular. Students should experience and understand basic tendencies, and understand the effect of changing the focal length. Students will also have the opportunity to change parts of the formula for a parabola and observe changes in the graph. Finally, students will see graphically that circular reflective mirrors can be used to approximate parabolic mirrors close to the vertex.

II. Performance or learner outcomes

Input the formula for a parabola into sketchpad.

Use a construct that allows them to control the angle of light coming in, the height of the focus, and the area of reflection to demonstrate the properties of various reflection devices.

Show that the focus of a spherical mirror is ½ the radius close to the vertex.

Show that a parabola and a circle are very similar at points close to the radius.

Use properties they know such as alternate interior angle theorem and properties of an isosceles triangle to make statements about the focus of a circle.

III. Resources, materials and supplies needed

2 Flipcharts - paper

Computer with projection for demonstrations

8 Computers for individual students all equipped with sketchpad.

Pre made sketchpad files.

Mice for all computers

IV. Supplementary materials, handouts. (Also address any safety issues

Concerning equipment used)

Handout - Sketchpad Activities

Five-E Organization

Teacher Does Probing Questions Student Does

Engage:

Learning Experience(s)

Depending on the Sketchpad experience level of students, do this as a group demo, or as an activity for individuals or pairs

Create a parabola by recreating the paper folding experiment

Basic Sketchpad info for new users:

1. If you get messed up, open a new copy of the file.

2. Use "Display"
"Trace" or

"Erase Traces"
to control tracings

If you highlight 2 things and try to move them, the whole graph will move.
Use "Edit" "Undo" to undo mistakes.

If students are not sketchpad trained, create the drawing as a demonstration to the group, then allow individual teams of 2 to play with them.

Approx. Time_10____mins

Critical questions that will establish prior knowledge and create a need to know

1.What are the first components?

(student should make these)

2. Where can we find the points of our parabola?

Expected Student

Responses/Misconceptions

1. A line and a point.

2. At the intersection of the vertical line above a certain point with the perpendicular bisector of the segment joining the point with the focus.

Student should construct these two items using sketchpad commands, and using the intersection, recreate the paper folding generation of a parabola.

Explore:

Learning Experience(s)

Investigations II - III

Approx. Time__20___mins

Critical questions that will allow you to decide whether students understand or are able to carry out the assigned task (formative)

See Handout - These investigations explore parabolic and circular reflections.

Grab the point of reflection (if you grab another part of the segment it will stretch weirdly-- use edit undo and try to get the point in the middle.) and move it around. Record the focus:

Now change the angle of light coming in. Light coming in straight is like light from an object directly in front of a telescope. Move N so that NOP is at an angle like 10 degrees. This will simulate light coming from an object that is not centered in the field of view. Now move the point of reflection and note the effects on the focus:

Remember, you cannot change the parabola by changing the focus on the picture, but you can change the focus by changing the formula -- double click on the formula and change the second number in the denominator.

Record your experiments and observations in the chart on the next page.

III.

1. What happens to the focus when P is at the side?:

2. What happens to the focus when P is at the bottom of the curve, close to A?:

3. Now use the diagram above, the three facts 1,2,3 and the remaining space on this page to say what the length of the focus is relative to the length of radius of the circle when P is close to A, and why this makes sense geometrically. A full proof is not required, but a path of logic and reason that uses the three facts above is needed.

Expected Student

Responses/Misconceptions

The focus is set at 10 initially

When light comes in from the left part of the field of view, it is reflected to the right of the center of focus.

When light comes in from the right part of the field of view, it is reflected to the left of the center of focus.

Students may change a from 10 to 4, and see the parabola get taller and thinner as the focus changes to 4, and so on.

Students may have trouble with sketchpad. If the trouble is big, work as a group with one computer.

When P is high on the sides of the circle, the focus is spread out.
When P is at the bottome of the curve, close to A, the focus is consistent, that is, exiting light goes to one point.
Here we hope students can see that, close to A, the focus is at ½ radius. We can show or prove this by noting that angle BPC must equal angle CPG by reflection, and angle ACP equals angle CPB so we have an isoscles triangle and PF = FC. As P approaches S, PF + FC = PC, so PC = 2xPF.

Explain:

Learning Experience(s)

Review Investigations I - III. Depending on the number of hangups, this may happen with quick hints while students are working, or it may evolve into a class demonstration if the facility with sketchpad is not adequate.

Approx. Time__10___mins

Critical questions that will allow you to help students clarify their understanding and introduce information related to concepts to be learned

What results did you get for Investigation II. What surprised you? What did you find that you were expecting.

What questions do you have.

Expected Student

Responses/Misconceptions

Students will hopefully do well with the activities. If there are no problems, students can be asked to make a systematic exploration of the parabola, changing only one parameter - the focus by changing the equation, or the angle of incoming light.

Extend / Elaborate:

Learning Experience(s)

Activity IV

Do as a group if students don't know sketchpad well

Approx. Time___5__mins

Critical questions that will allow you to decide whether students can extend conceptual connections in new situations

This activity asks students to consider how and whether parabolic and spherical mirrors can be used to do the same jobs.

Expected Student

Responses/Misconceptions

Students should find that for a larger diameter, a circle will approximate a parabola and vice versa for points near the bottom, or vertex of the drawing.

Evaluate:

Lesson Objective(s)

Learned (WRAP –UP at end) -> Summarize

Ongoing evaluations will happen as teacher circulates, or as the need to make procedural announcements arises.

Approx. Time_____mins

Critical questions that will allow you to decide whether students understood main lesson objectives

The number of questions, and rate of progress on the Activities will say a lot about the students ability to learn by exploring with GSP.

Expected Student

Responses/Misconceptions

The biggest issue is likely to be trouble with Sketchpad.

Sketchpad Activities

I. Construct a Parabola: Activity or Group Demonstration

Start by placing a point on the screen, this will be the focus

Next place two points horizontally on the bottom of the screen. Construct a line which will be the Directrix.

Place a point on the Directrix line, and call it D.

Highlight the Directrix and the point and construct a perpendicular.

Now Highlight point D and the focus, and construct a segment. Highlight the segment, construct a midpoint. Highlight the segment and the mid point, and construct a perpendicular.

Highlight the two perpendiculars, and construct the intersection. This is a point on the parabola.

I. Exploring a Parabola - Open the file labeled "Sketchpad Lesson 1 Parabola"

Mark the point, P you just found with “trace” and move D around on the Directrix. You should trace out a parabola. Or mark the line which is tangent to the parabola - the "crease" in our paper folds, and set the whole line to trace. You will see an image just like our paper folding.

Move the focus up or down, erase traces and move D again to see a new parabola.

Questions/ Observations:

What happens when you move the focus, farther from or nearer to the Directrix?

Record at least one more observation:

II. Open the file labeled "Sketchpad Lesson 2 - Focus of Parabola"

This file will show what happens when light hits a parabolic mirror. The formula provides a parabola. We then pretend the parabola is reflective, or a mirror, and we want to investigate its properties.

The little segment at the point of reflection approximates the tangent, and allows us to show how the incoming rays might reflect around the perpendicular at any point. As you move the point of reflection, the outgoing ray will trace its path.

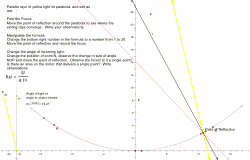
Locate the "light control" on the left side of the screen. Move point N until it is over P. The light will come in straight, and the measure of angle NOP will be at or close to 0.

Use "display" "erase traces" to clear the screen.

Grab the point of reflection (if you grab another part of the segment it will stretch weirdly-- use edit undo and try to get the point in the middle.) and move it around. Record the focus:

Now change the angle of light coming in. Light coming in straight is like light from an object directly in front of a telescope. Move N so that NOP is at an angle like 10 degrees. This will simulate light coming from an object that is not centered in the field of view. Now move the point of reflection and note the effects on the focus:

Record your experiments and observations in the chart on the next page:

Parabola Equation	Angle of incoming light	Observations of focus, location, etc.

IV. Open the file called Sketchpad Lesson 3 - Spherical Lens

Record your answers to the questions below.

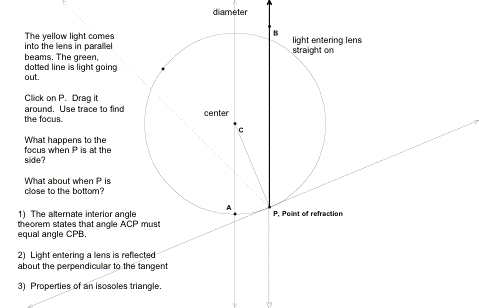
What happens to the focus when P is at the side?:

What happens to the focus when P is at the bottom of the curve, close to A?:

Now use the diagram above, the three facts 1,2,3 and the remaining space on this page to say what the length of the focus is relative to the length of radius of the circle when P is close to A, and why this makes sense geometrically. A full proof is not required, but a path of logic and reason that uses the three facts above is needed.

IV. Reopen the File Parabola File 1

We have already seen that a circular mirror can also focus light within a range of reflective points near the vertex of the lens.

If the formula has not been changed, the focus of the construct is at 10. We have just discovered that for a circle, the lens can focus well at a point which is ½ the radius. Make a circle with radius 20, and center (0, 20) and compare the physical properties of a circle with center (0,20) and radius 20.

What do you observe?

Can we use spherical mirrors to focus light? In which cases-all or just for some types?