PBI Telescope Preparation (1)
LESSON PLAN # _Part 1 - no computer ClassDay/Time 10:45-11:15__________
Technology Lesson? No
Name: Lauren Siegel
Title of lesson: Construction of a Parabola
Date of lesson:
Length of lesson: 45 minutes
Description of the class:
Name of course: Algebra II
Grade level: 11th Grade
Honors or regular: Regular
Source of the lesson:
Mark Daniels - paper folding activity
Sullivan, Michael, Precalculus Prentice Hall Chapter 9 p. 668.
Diagrams made in Geometer Sketchpad.
TEKS addressed:
(b) Foundations for functions: knowledge and skills and performance descriptions.
(1) The student uses properties and attributes of functions and applies functions to problem situations. Following are performance descriptions.
(A) For a variety of situations, the student identifies the mathematical domains and ranges and determines reasonable domain and range values for given situations.
(3) The student formulates systems of equations and inequalities from problem situations, uses a variety of methods to solve them, and analyzes the solutions in terms of the situations. Following are performance descriptions.
(C) For given contexts, the student interprets and determines the reasonableness of solutions to systems of equations or inequalities.
(c) Algebra and geometry: knowledge and skills and performance descriptions.
(1) The student connects algebraic and geometric representations of functions. Following are performance descriptions.
(A) The student identifies and sketches graphs of parent functions, including linear (y = x), quadratic (y = x2), square root (y = … x), inverse (y = 1/x), exponential (y = ax), and logarithmic (y = logax) functions.
(B) The student extends parent functions with parameters such as m in y = mx and describes parameter changes on the graph of parent functions.
(C) The student recognizes inverse relationships between various functions.
(2) The student knows the relationship between the geometric and algebraic descriptions of conic sections. Following are performance descriptions.
(B) In order to sketch graphs of conic sections, the student relates simple parameter changes in the equation to corresponding changes in the graph.
(C) The student identifies symmetries from graphs of conic sections.
(D) The student identifies the conic section from a given equation.
(B) The student relates representations of quadratic functions, such as algebraic, tabular, graphical, and verbal descriptions.
(C) The student determines a quadratic function from its roots or a graph.
(2) The student interprets and describes the effects of changes in the parameters of quadratic functions in applied and mathematical situations. Following are performance descriptions.
(B) The student uses the parent function to investigate, describe, and predict the effects of changes in a, h, and k on the graphs of y = a(x - h)2 + k form of a function in applied and purely mathematical situations.
(C) The student compares and translates between algebraic and graphical solutions of quadratic equations.
Source: The provisions of this ¤111.33 adopted to be effective September 1, 1996, 21 TexReg 7371.
I. Overview
Students will do a brief engagement activity where they construct a parabola through paper folding. Second, the paper folding activity will be related to a general proof that the points determined meet the definition of the definition of a parabola. Parts of the parabola will be discussed and defined. Finally, a parabola is placed on the coordinate plane, and students derive the general formula.
II. Performance or learner outcomes
Students will be able to:
State the definition of a parabola
Sketch a parabola and label the focus and directrix
Superimpose a coordinate axis on a parabola, focus and Directrix and derive the formula y=x^2/4a
Explain how the graph alters for different values of a
III. Resources, materials and supplies needed
Two Paper easels at minimum
Wax paper for activity
No. 2 pencils
Rulers.
Handouts
String and pen
Colored pens for easel
Meter Stick
IV. Supplementary materials, handouts. (Also address any safety issues
Concerning equipment used)
Five-E Organization
Teacher Does Probing Questions Student Does
|
Engage: Learning Experience(s)
Review concepts from preview sheet. Take any questions. Students should review these concepts prior to this lesson.
Midpoint
Perpendicular Bisector
Distance Formula
Definition: Distance of a point to a line
Reflection about an axis.
Approx. Time___5__mins |
Critical questions that will establish prior knowledge and create a need to know
1a. What is the definition of a midpoint?
1b.If no answer, draw two points, and label them A and B on the board and the segment in between. Wait for suggestions. Allow a volunteer to identify the midpoint. Ask the students what letter we-mathematicians usually designate midpoints
2a. Now we have a line segment AB. Can we find the
perpendicular to segment S through M? 2b. Optional Ð if time is short, just sketch perpendicular. Explain that it can be sketched, but also a proof and method exists for finding a midpoint, and the perpendicular using a string for a compass and. Ask if anyone knows how to do this.
2c. What are the main features of the perpendicular bisector? What do we know about it?
3a. Distance Formula. Can someone state it?
3b. Given two points with coordinates (a,b) and (c,d) what is the distance between them?
4a. What is the distance from a point to a line? (Sketch a line and a point?)
4b. If needed continue with these questions: Is it on a diagonal? or along a squiggle? Draw some options.
5a. From this morning, what is a reflection?
Ask a student to draw a picture.
Also draw a curved surface.
|
Expected Student Responses/Misconceptions
1a. The center point of a line segment.
1b. The center point on the line segment.
The midpoint is often labeled M. This is a convention, and it could be any convenient letter that distinguished it from other points in a diagram.
2a. Yes just draw it.
2b. A student may know how to draw the perpendicular bisector. If not, demonstrate.
2c. Any point on the bisector is equidistant from each endpoint.
3a. Student writes the distance formula.
3b. Ã[(a-c)^2 + (b-d)^2] = D
4a. The shortest distance, along the perpendicular to the line through the point.
4b. Students should see that it is the shortest distance, along a perpendicular.
5a. A mirror image, or light bouncing of a surface.
Hopefully a student will draw a reflective surface (line) and he path of a ray that hits the line at an angle and bounces back along a path that is at the same angle, but opposite side to a perpendicular drawn through the point of reflection.
Students should recall that a curved surface bends light with respect to the perpendicular, and that a curved surface can have a focus where exiting light rays converge.
|
Explore: Learning Experience(s)Students will be counted off as l, 3, 5.
Write the definition of a parabola on one flipboard:
A parabola is the set of points in the plane that are the same distance from a fixed point F as they are from a fixed line D. The fixed point is called the Focus, and the fixed line is called the Directorix.
Activity: Give each student a sheet of wax paper, a ruler and a pencil. Directions: á Place a line on the lower quarter of the paper -- demonstrate on a second flip chart. á Place about ten points on the line á Place a point on the paper low, medium or high above the line á Fold the paper so a point on the line is over the point you drew. Make the crease. Unfold the paper and, using the ruler, draw a line in the crease. Demonstrate with second Flip Chart
Repeat for various parts of the line
Wait 5-10 minutes.
Ask students to compare their result with their neighbors.
Wait 2 minutes
Approx. Time____15_mins |
Critical questions that will allow you to decide whether students understand or are able to carry out the assigned task (formative)
1. Ask students if they have seen this definition and terms before?
Ask students if they understand the directions
Ask students to raise their hand if they need help, but otherwise begin the activity.
2. Ask students what they made.
3. Ask students who were ls to hold up their result. Next 3s, then 5s.
What do you notice?
Show some student samples from each category.
4. What about this method? Why are the directions so loose --- should they be more exact? Why or why not?
Optional.
Ask students to measure the distance from their line to the focus, or original point and write the number in cm on the upper right hand
Collect several papers and order by distance. Display in order. Have students come to table to observe.
|
Expected Student Responses/Misconceptions
1. Students respond with whatever experience they have.
2. A bunch of lines that make a parabola.
3. The 1's are tall skinny parabolas and the 3's are wider and flatter. The 5's are the widest and flattest.
4. The directions do not have to be exact. All that matters is that the line is over the dot when the fold is made.
|
|
Explain: Learning Experience(s)
Proof. Here we will relate the paper folding to the components of a geometric proof.
First, letÕs discuss what we did with the paper. Draw on flipchart 2.
Ask students to reread the definition of a parabola still displayed on board 1.
Now ask students to draw a vertical line from that same point.
Be sure students notice that we go through the process of finding a perpendicular bisector and perpendicular to the Directrix uniquely for each point on the Directrix.
Approx. Time_15____mins |
Critical questions that will allow you to help students clarify their understanding and introduce information related to concepts to be learned
1. Take a look at your wax paper model. Draw a line real or imagined from one of the points on the Directrix (line) to the focus. Redo that fold -- what do you observe?
2.
Do we have a name for a point halfway between two endpoints? 3. What about the line we drew in the crease?
4. If the fold is the perpendicular bisector of the segment AF, what does that tell us about the points on the line in the crease?
4a. Does
this mean that all the points on all the fold lines are part of the parabola?
Why?/Why not?
5. How does the requirement that the parabola points be equidistant from a point and a line affect which points meet the definition?
6. Which points meet the definition of parabola?
|
Expected Student Responses/Misconceptions
4. The points on the crease are all equidistant from the endpoints A and F.
4a. Students may think either is true. Encourage some discussion. ( Point out if a student does not that the midpoints of each folding proceedure actually lie on a line.)
5. Students will hopefully say that because the distance to a line is always on the perpendicular, that for a given point on the line, the parabola point must lie on the perpendicular to the line at that point.
6. Just the points that are equidistant from the Focus and Directrix - eg. For a point X on the Directrix, the parabola point is located on the perpendicular to the Directrix and also on the Perpendicular bisector to the segment FX. |
|
Extend / Elaborate: Learning Experience(s)
Now we can take the informal geometric proof and use it to generate the formula for a parabola.
Pass out the worksheet. Take a look at the sheet.
The parabola is already drawn -- it could be a copy of one of the ones we generated with the paper folding.
[Rather than talk students through this portion, we will for the sake of time give them the set up of the coordinate axes with the vertex of the parabola at (0,0).]
Preview Worksheet:
Give a brief overview of the sheet. In particular, ask students if they understand the assignment of the height "a" to the focus, and how that affects the coordinates of the focus. Also mention that D here is a point even though we used it in the distance formula to represent Distance.
Approx. Time_____mins
|
Critical questions that will allow you to decide whether students can extend conceptual connections in new situations
1. Now we want to place our parabola on the coordinate plane and describe it with an equation? What are we trying to do?
2. One way we can do this is to let the bottom or vertex of the parabola be at (0,0), and so the focus will fall on the y-axis. Could we do it another way?
Note - numbering starts over to match worksheet.
1.
We already have the vertical line through D on the Directrix.
Draw a line from D to the Focus, and sketch the perpendicular bisector. It
should go through P -- Does it? 2. The axes will form a coordinate grid. Assume that the vertex or bottom of the parabola is at the point (0,0).
Let the
coordinates of P be (x,y).
q What is the coordinate of the Focus? ________________
q What is the coordinate of D? ______________________
q What is the equation of the Directorix? ____________________
3.
What do we know about the distance from the Focus to P as it
relates to the distance from P to
D?___________________________________________________ 4. Recall the distance formula: Given two points with coordinates (a,b) and (c,d) the distance between them is Ã[(a-c)^2 + (b-d)^2] )
Distance from P to the
Focus:________________________________
7) Now set your answers equal to each other and solve for y:
Distance from P to the Focus = Distance from P to D
This result is the basic equation of a parabola. We will explore this equation further with a sketchpad activity in the next half hour.
|
Expected Student Responses/Misconceptions
(circulate to verify)
The focus is at (0,a)
D is at (-a,x)
x=-a
The distances are the same
P: (x,y) Focus: (0,a)
Distance = (x^2 +(y-a)^2)^.5
P: (x,y) D: (x,-a)
Distance = ((y+a)^2)^.5
x^2+y^2-2ay+a^2=y^2+-2ay+a^2
x^2 - 2ay = 2ay y = x^2/(4a) |
|
Evaluate: Lesson Objective(s) Learned (WRAP ÐUP at end) -> Summarize
Do this activity if there is time. The mirrors we use are spherical, but we will see in the sketchpad activity that parabolic and spherical mirrors behave similarly close to the vertex.
Students will be given a chart to find all four parabola equations on their own as homework. They should be able to do this.
Approx. Time__N/A___mins |
Critical questions that will allow you to decide whether students understood main lesson objectives
Now that we have the equation of a parabola, if we have a parabolic mirror that has height ______ -measure height of telescope mirror, and diameter ______ calculate the location of the focus - in other words, find a.
Be sure to center your parabola on the coordinate grid to find the appropriate x and y that go into your parabolic equation.
Students are asked to make some comparative statements about the four parabola equations. |
Expected Student Responses/Misconceptions
Students may not be ready to make this attempt without guidance. Depending on time do as a group activity, or allow them to attempt in pairs.
The answer is to halve the diameter of the mirror, to get an x value, and use the height from bottom to top of curve for y so:
Y = x^2/4a -- plug in radius for x and height for y and solve for a. a will be distance above (0,0) on the y axis.
Not all students will be successful. Computation errors can be a problem, as well as making a mistake in the assignment of coordinates. |
Name___________________________________________
Equation of a Parabola
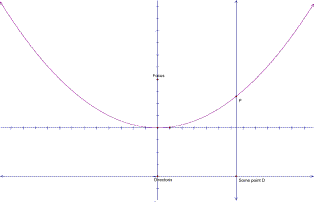
- We already have the vertical
line through D on the Directrix. Draw a line from D to the Focus, and
sketch the perpendicular bisector. It should go through P -- Does it?
____________
- The axes will form a coordinate grid. Assume that the vertex or bottom of the parabola is at the point (0,0). [label this on the graph]
Let the
coordinates of P be (x,y), and label
graph accordingly.
Let the distance from the vertex to the focus be an unknown, and variable -- called
it a.
Find representations for the following:
¤ What is the coordinate of the Focus? ________________
¤ What is the coordinate of D? ______________________
¤ What is the equation of the Directrix? ____________________
- What do we know about the distance from the Focus to P as it relates to the distance from P to D :
__________________________________________________
- Recall the distance formula:
Given two points with coordinates (a,b) and (c,d) the distance between
them is Ã[(a-c)^2 + (b-d)^2] ) to find:
Distance from P to the
Focus:________________________________
Distance from P to D:_______________________________________
- Now set your answers equal to each other and solve for y:
This result is the basic equation of a parabola. We will explore this equation further with a sketchpad activity in the next half hour.
Preview Sheet - Terms and Definitions
Midpoint
Given two points, A and B, we can draw a line segment between them and call it segment AB. The point exactly halfway between A and B is the midpoint, often designated by the letter M.
![]()
We can also say equivalently that M is the midpoint of AB means that AM = MB, that is the distance between A and M is the same as the distance between M and B.
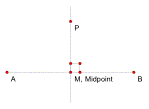
Perpendicular Bisector
The perpendicular bisector of a segment is the line through the midpoint that intersects the segment at a 90 degree angle. All of the points, P on the bisector are equidistant from both A and B. That is, AP=PB
Distance Formula
The distance between any two points in a coordinate plane can be calculated using the distance formula. Let the first point have coordinates (a,b) and the second point be at coordinate (c,d), the formula states:
![]() The
distance between the points (a,b) and (c,d) is:
The
distance between the points (a,b) and (c,d) is:
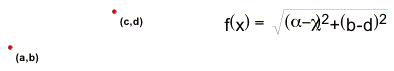
Definition: Distance of a point to a line
The distance from any point to a line is always the shortest distance which is along the perpendicular (eg above the distance from P to the line segment AB is the distance from P to M because M is on the line perpendicular to AB which goes through P.
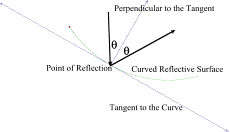 Reflection about an
axis. A line or ray reflects at an angle,
call it theta, equal to the angle of entry to but on the opposite side of the
perpendicular to the surface at the point of reflection
Reflection about an
axis. A line or ray reflects at an angle,
call it theta, equal to the angle of entry to but on the opposite side of the
perpendicular to the surface at the point of reflection
Wax Paper Folding Activity
q Draw a line somewhere on the bottom quarter of your wax paper.
q Place a point, centered left-right, or not too far from centered (so you get the whole pattern) somewhere above the line.
q If the class is divided into groups, and you are a 1, place your point close to the line, if you are a 3, maybe around 3 cm and if you are a 5, somewhere closer to 5 cm.
.
Examples: Your paper will look something like one of these examples, depending on how high you place your floating dot. Please note that the placement of the dots is not exact.

q This part needs to be exact. Fold the paper so that the line is over the dot. Make a crease in the paper, then use your ruler to draw a line where the crease is. Repeat using different parts of the line until a pattern emerges.
Name________________________________
Derive the basic parabola equation for each of the four examples. Show work on a separate sheet, or the back:
|
Vertex |
Coordinates. Vertex |
Coordinates Focus |
Equation Directrix |
Equation of Parabola |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
On the back of this sheet, write down at least two observations about parabolas and the formulas you derived.




