Mean, Median, Mode, and Standard Deviation

Name(s): Katie May

Title of lesson: Mean, Median, Mode, and Standard Deviation

Date of lesson: Thursday and Friday of Week 1

Length of lesson: 2 45-minute periods

Description of the class:

Name of course: Algebra II

Grade level: 8-9^h grade

Honors or regular: Regular

Source of the lesson:

Ron Larson, Laurie Boswell, Timothy D. Kanold, and Lee Stiff’s Algebra 2

http://geography.about.com/od/populationgeography/a/lifeexpectancy.htm

www.census.gov/population/projections/MethTab2.xls

TEKS addressed:

b(2A.1)  Foundations for functions. The student uses properties and attributes of functions and applies functions to problem situations.

The student is expected to:

(A) identify the mathematical domains and ranges of functions and determine reasonable domain and range values for continuous and discrete situations; and

(B) collect and organize data, make and interpret scatterplots, fit the graph of a function to the data, interpret the results, and proceed to model, predict, and make decisions and critical judgments.

I. Overview

Students will learn about basic statistical analysis and measures of central tendency. Specifically, students will be able to find the mean, median, mode, and standard deviation of a given set of data. If students have previously learned this material, more emphasis can be placed on making predictions based on data and creating statistical graphs.

II. Performance or learner outcomes

Students will be able to:

· Mean of a data set

· Median of a data set

· Mode of a data set

· Standard deviation of a data set

III. Resources, materials and supplies needed

· 1 calculator per group

· 1 piece of graph paper per group

· 1 pencil per student

· 1 note card per student

· 1 textbook per student

IV. Supplementary materials, handouts. (Also address any safety issues

Concerning equipment used)

· 1 print out of the first website listed above per student (copied in Appendix A) or access to a computer

· 1 print out of the second website listed above per student (the necessary portion copied in Appendix B) or access to a computer

V. Safety Issues

· While there are no specific safety issues, safe classroom procedures should be used with pencils, calculators, and other materials.

Five-E Organization

Day 1

Teacher Does Probing Questions Student Does

Engage: Approx. Time_5__mins

What do you think the average age of death is for a person in the United States? What about the world? Why do you think people in some countries live longer than other countries?

Student will give various answers such as 60, 70, and 80. Students will probably give similar answers to the first questions but might say lower ages such as 50 and 55. Students might say that some countries are healthier, cleaner, and have better medical options while others are not as healthy and do not have as many resources.

Explore: “Well, today and tomorrow we will be looking at average life expectancy and be answering some of these questions. We are going to start by reading an article about life expectancy. I would like you to read the article and then pair up with a partner to discuss what you learned and questions you still have about life expectancy.” Teacher passes out the article in Appendix A for students to read. Approx. Time__15_mins

Students read the article and talk with a partner about what they learned from the article and what question they still have about life expectancy.

Explain: The teacher leads a discussion of what the students learned in the article. Approx. Time_5___mins

What are some things you learned? The article mentioned many average life expectancies for different countries. What is an average? How do you come up with an average?

Students will most likely state various points of the article, such as the low life expectancies of some countries and very high life expectancies of others. “The middle.” “The most.” “What you expect.” Student will probably give various answers and have some misconceptions about average. “Adding numbers together and then dividing.” “Surveying people.” “Using math.”

Extend / Elaborate: The teacher gives an explanation about mean, median, and mode based on page 445 of the textbook. The teacher should give a clear explanation of the definition of each word as well as how to find the mean, median, and mode. The teacher should help clear any misconceptions stated in the “Explain” section. The teacher should point out that these are all a part of statistics and are called measures of central tendency. They are used to help summarize and compare sets of data. Approx. Time__15__mins

Is the average the number that is in the middle of the data set? Is the average the number that happens the most in the data set? Do the words mean and average mean the same thing?

No, that is the median. No, that is the mode. Yes.

Evaluate: Teacher asks students to fill out a “Minute Paper.” On a note card they should write one thing they learned and one question they still have about life expectancy or mean, median, and more. The teacher also assigns the students to read page 445 of their textbook for homework. Approx. Time_5___mins

Students fill out a note card with one thing they learned and one question they still have.

Day 2

Teacher Does Probing Questions Student Does

Engage: Approx. Time_5__mins

Yesterday, we talked about mean, median, and mode. In light of our unit, “Will you live to be 110?,” why do think it would be helpful to know the mean, median, and mode of life expectancy?

“To see how long people normally live.” “So we can tell if most people live to be a certain age.” “To help us see how other factors affect life expectancy.”

Explore: The teacher explains that today the students will be working with information from the census bureau about life expectancies by state. Before splitting the class into groups of three, the teacher gives the following instructions: Each group will be given the table in Appendix B. The students will need to find the mean, median, and mode of the data, as well as graph a histogram on a sheet of graph paper. One student will be the “Calculator” of the mean, median, and mode. One student will be the “Recorder” of the mean, median, and mode. One student will be the “Graph-er” of the data. Even though each person has a specific role, all the group members need to collaborate to find the answers and draw a histogram. Approx. Time_15__mins

Students find the mean, median, and mode of the data. Students draw a histogram on a piece of graph paper.

Explain: The teacher asks each “Recorder” to come up to the board and write the mean, median, and mode they found. They should also draw a small histogram. Approx. Time__10__mins

What was the mean of the states’ life expectancies? What was the median of the states’ life expectancies? What was the mode of the states’ life expectancies? Why was there no mode?

76.9 77.3 There wasn’t one. Each life expectancy was different.

Extend / Elaborate: The teacher explains that there is another measure of central tendency called standard deviation. The teacher explains the formula for standard deviation and asks students to start to calculate the standard deviation for the data in their groups. The students can look at page 446 in their textbook for help. Approx. Time__10__mins

The students begin to work on finding the standard deviation for the data in groups.

Evaluate: The students are to continue calculating the standard deviation at home for homework and bring back the standard deviation they found the next day. Approx. Time__5__mins

For homework, the students will finish finding the standard deviation, which is 1.52 years.

· Note: Some classes may finish the Day 1 activities early and can move on to the Day 2 exploration. This will allow more time for the students to begin calculating the standard deviation on Day 2.

Appendix A

Life Expectancy

http://geography.about.com/od/populationgeography/a/lifeexpectancy.htm

From Matt Rosenberg

Jan 3 2006

Life expectancy from birth is a frequently utilized and analyzed component of demographic data for the countries of the world. It represents the average life span of a newborn and is an indicator of the overall health of a country. Life expectancy can fall due to problems like famine, war, disease and poor health. Improvements in health and welfare increase life expectancy. The higher the life expectancy, the better shape a country is in.

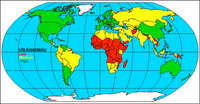
As you can see from the map, more developed regions of the world generally have higher life expectancies (green) than less developed regions with lower life expectancies (red). The regional variation is quite dramatic.

However, some countries like Saudi Arabia have very high GNP per capita but don't have high life expectancies. Alternatively, there are countries like China and Cuba that have low GNP per capita have reasonably high life expectancies.

Life expectancy rose rapidly in the twentieth century due to improvements in public health, nutrition and medicine.

It's likely that life expectancy of the most developed countries will slowly advance and then reach a peak in the range of the mid-80s in age. Currently, microstates Andorra, San Marino, and Singapore along with Japan have the world's highest life expectancies (83.5, 82.1, 81.6 and 81.15, respectively).

Unfortunately, AIDS has taken its toll in Africa, Asia and even Latin America by reducing life expectancy in 34 different countries (26 of them in Africa). Africa is home to the world's lowest life expectancies with Swaziland (33.2 years), Botswana (33.9 years) and Lesotho (34.5 years) rounding out the bottom.

Between 1998 and 2000, 44 different countries had a change of two years or more of their life expectancies from birth and 23 countries increased in life expectancy while 21 countries had a drop.

Sex Differences

Women almost always have higher life expectancies than men. Currently, the worldwide life expectancy for all people is 64.3 years but for males it's 62.7 years and for females life expectancy is 66 years, a difference of more than three years. The sex difference ranges from four to six years in North America and Europe to more than 13 years between men and women in Russia.

The reasons for the difference between male and female life expectancy are not fully understood. While some scholars argue that women are biologically superior to men and thus live longer, others argue that men are employed in more hazardous occupations (factories, military service, etc). Plus, men generally drive, smoke and drink more than women - men are even more often murdered.

Historic Life Expectancy

During the Roman Empire, Romans had a approximate life expectancy of 22 to 25 years. In 1900, the world life expectancy was approximately 30 years and in 1985 it was about 62 years, just two years short of today's life expectancy.

Aging

Life expectancy changes as one gets older. By the time a child reaches their first year, their chances of living longer increase. By the time of late adulthood, ones chances of survival to a very old age are quite good. For example, although the life expectancy from birth for all people in the United States is 77.7 years, those who live to age 65 will have an average of almost 18 additional years left to live, making their life expectancy almost 83 years.

Appendix B

Table 2: Average Life Expectancy at Birth by State for 2000 and Ratio of Estimates and Projections of Deaths: 2001 to 2003
State	Life expectancy at birth Total
Alabama	74.6
Alaska	76.7
Arizona	77.5
Arkansas	75.1
California	78.3
Colorado	78.4
Connecticut	78.4
Delaware	76.6
District of Columbia	72.6
Florida	77.5
Georgia	75.3
Hawaii	79.8
Idaho	78.0
Illinois	76.7
Indiana	76.2
Iowa	78.5
Kansas	77.5
Kentucky	75.3
Louisiana	74.4
Maine	77.6
Maryland	76.3
Massachusetts	78.4
Michigan	76.5
Minnesota	79.1
Mississippi	73.7
Missouri	76.2
Montana	77.3
Nebraska	78.3
Nevada	75.9
New Hampshire	78.5
New Jersey	77.5
New Mexico	77.3
New York	77.9
North Carolina	75.8
North Dakota	78.7
Ohio	76.4
Oklahoma	75.3
Oregon	77.9
Pennsylvania	76.8
Rhode Island	78.2
South Carolina	74.9
South Dakota	78.0
Tennessee	75.0
Texas	76.7
Utah	78.7
Vermont	78.2
Virginia	76.9
Washington	78.2
West Virginia	75.0
Wisconsin	78.1
Wyoming	77.1
Footnote:
U.S. Census Bureau, Population Division, Interim State Population Projections, 2005.
Internet Release Date: April 21, 2005