Name(s): Sheila Ogden

Title of lesson: A very slippery Slope

Length of lesson: 50 minutes

Description of the class:

Name of course: Algebra

Honors or regular: either

TEKS addressed:

2) The student understands the meaning of the slope and intercepts of linear functions and interprets and describes the effects of changes in parameters of linear functions in real-world and mathematical situations.

A) The student develops the concept of slope as rate of change and determines slopes from graphs, tables, and algebraic representations.

B) The student interprets the meaning of slope and intercepts in situations using data, symbolic representations, or graphs.

C) The student investigates, describes, and predicts the effects of changes in m and b on the graph of y = mx + b.

Objective

The students will understand how to identify the slope of a line.

The Students will be able to:

1) Measure the slope of a given line.

2) Deduce the slope of a line connecting two points when given any two points in a coordinate plane.

Resources, materials and supplies needed

· Pencil, meter stick, graph paper

IV. Supplementary materials, handouts. (Also address any safety issues

Concerning equipment used)

Homework and overhead handouts as stated

Teacher Does Probing Questions Student Does

Engage: Ask, ‘When driving down a hill which is steeper, a 6% grade or a 10% grade?” Introduce the idea of rise over run.. 10 minutes

What does grade mean? Can you draw it out? What are you calculating? How would the gradient change in different circumstances?

It looks at not only the decent but how long it takes to make the decent. Grade represents the decent over a certain period of time

Explore: After discussing this explain to students that we are going to be looking at different inclines. Put students into groups and travel with them to various stairwells on campus. 15 minutes

Students travel around the building measuring different stair cases. In looking at how far up you go versus how fast you do it.

Maybe we can look at a general change in the points.

Explain: Students reconvene in the classroom and as a class discuss findings. Graphs work much the same way. While they are all progressing over a domain and range, they can do it at different rates. How can this idea of the stairs be extended to graphs? When we look at this change in reference to a graph it is called the slope. 20 minutes

What did we notice about these different stair cases? But they are all stairs, how are they different? How do the stairs mirror this? (look at linear equation graphed on board) How can we calculate this? Teacher connects points and drops lines to connect them making a right triangle. Introduces the formal notation of y-y x-x

They are different Students note that some take you higher than others. Some aren’t as long, and don’t raise you as high. Students propose ideas. Students realize the link of this triangle to what they already know about the hypotenuse of a right triangle in the Pythagorean theorem.

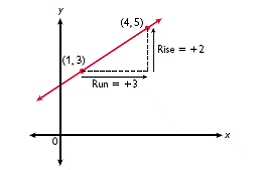
Extend / Elaborate: Look at first point on over head (4,5) and (1,3).

What is the slope between them? Is the slope always positive? What is an example of when the slope of a line would be negative? Can we draw that? We call lines with negative slopes decreasing and lines with positive slopes increasing. How do we know which point to start with in calculating slope?

No, it’s not always positive. When the line is going down (decreasing). It doesn’t matter as long as the x value is taken with the corresponding y value.

Evaluate: Look at these points on the overhead, draw their lines and find the slope. Teacher hands out homework to be graded following day

Teacher draws points on overhead not showing actual overhead until answers are shared How did we calculate this?

Overhead

http://www.glencoe.com/sec/math/mathscape/2005/course3/additional/pdfs/FamilyPortraits/phase2.pdf

Homework

(KEY)

Graph the following equations and find their slope.

1)

This is the graph of y=2x. It has a slope of two and passes through the point (2,4).

2)

This is the graph of y=4x. We can see that the graph is increasing (at a greater rate).


3)

This is the graph of y=(1/2)x. We can see that the graph is increasing (at a lesser rate).

4)

This is the graph of y=-5x. We can see the graph is now decreasing.

5)

This is the graph of y=0x+3. We can see that a graph with a slope of 0 is horizontal.

http://jwilson.coe.uga.edu/EMT669/Student.Folders/Cronic.Drew/Teaching%20Unit.html