Fibonacci Sequence

LESSON PLAN # _______ ClassDay/Time__________

Technology Lesson? Yes No (circle one)

Name(s): Rachel Carroll

Title of lesson: Bunnies, Bunnies, and more Bunnies (Seqences/Patterns)

Date of lesson: Fourth week of project

Length of lesson: 50 - 90 min

Description of the class:

Name of course: Geometry

Grade level: 9-10

Honors or regular: regular

Source of the lesson:

Websites:

http://school.discovery.com/lessonplans/programs/numbersnature/

http://www.mathsisfun.com/numberpatterns.html

TEKS addressed:

High School Geometry

B.2 (A) The student uses constructions to explore attributes of geometric figures and to make conjectures about geometric relationships.

B.3 (B) The student constructs and justifies statements about geometric figures and their properties.

(D) The student uses inductive reasoning to formulate a conjecture.

C. (1) The student uses numeric and geometric patterns to make generalizations about geometric properties, including properties of polygons, ratios in similar figures and solids, and angle relationships in polygons and circles.

F. (2) The student uses ratios to solve problems involving similar figures.

I. Overview

Students will find that math is seen in nature. It may not be perfect, but you can see patterns and notice relationships. Given a starting point they can struggle as Fibonacci once did, yet with a positive end result. Answers are not always given in our world and the students need to see that even though something might look abstract, there may still be some pattern that is mathematical.

II. Performance or learner outcomes

Students will be able to:

Recognize a sequence

Continue a sequence

Understand the Fibonacci sequence

Find Fibonacci sequence in nature

III. Resources, materials and supplies needed

ruler

compass

worksheets

flower petals, seed heads, cauliflower florets, pinecones, apple (if possible)

IV. Supplementary materials, handouts. (Also address any safety issues

Concerning equipment used)

Use the website Common Number Patterns for ideas of patterns to use in the Engage section of the lesson.

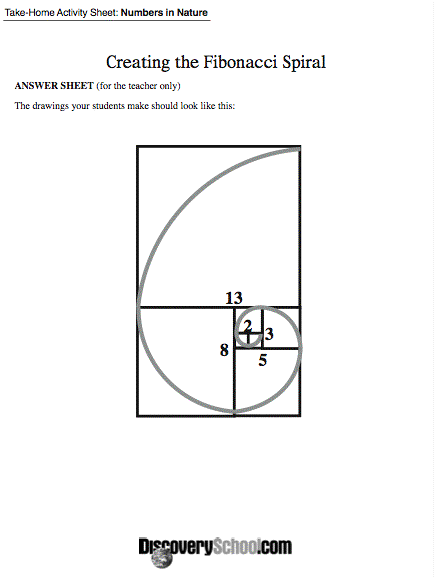
Finding Fibonacci Numbers in Nature (in class)

Creating the Fibonacci Spiral (take-home)

V. Safety Issues

none

VI. Accommodations for learners with special needs (ELLs, Special Ed, 504, G&T)

For accelerated students, given a sequence of numbers, have them produce the function that represents the sequence. Show a couple examples and have them discover the remaining patterns. This can be either a project or a take home activity. A computer with Excel capabilities is ideal for this so that every set of computations goes faster.

Five-E Organization

Teacher Does Probing Questions Student Does

Engage: Draw patterns on the board and assign one per group (put students in groups of 3 or 4) Look at the website Common Number Patterns Approx. Time__10__mins	What patterns do you see? How could you represent this mathematically? What would be the next 3 numbers in the sequence?	Students may take a little time finding the sequence pattern, so go to them individually to help out. Let groups help each other if they can lend ideas.
Evaluation(Decision Point Assessment):	One student from each group will show their results on the board.	Students can provide the next three numbers in the sequence. If they cannot have all groups solve the problem and lead them to the answer if they still cannot get it. Then try another problem until they get the concept of sequences/patterns.

Explore: Fibonacci – Discuss the history of the Fibonacci sequence (Leonardo F. 1202 decided to investigate how fast rabbits could breed). Beginning with one breeding pair, and knowing that rabbits can mate when one month old and each female can give birth to another pair of rabbits. Look at how many pairs of rabbits exist each month. Continue this pattern for 3 months. Approx. Time__15__mins	Continue the story for the rabbits and find a sequence in your groups. What pattern do you see? How do you get this pattern?	Students may try to count each rabbit instead of mating pairs of rabbits. Students may not understand how to get the next number so tell them to continue the process with the rabbits and not to guess the next number.
Evaluation(Decision Point Assessment):	Number sequence continued beyond what was done on the board, ideally up to 15 numbers.	Students should have the drawing of the rabbit breeding expansion completed next to the number sequence.

Explain: Discuss the pattern with the whole classroom and hand out the worksheets that have them discover the Fibonacci sequence in nature (flower petals, seed heads, cauliflower florets, pinecones, apple) Pass out homework (not to be done in class). Approx. Time__10__mins	Are there other places in our world where we can find this pattern besides breeding rabbits? Look at the worksheets (do your own but you can collaborate) to find the Fibonacci sequence in these objects of nature. What shape emerges from clusters of seeds? (the spiral – explain that this an efficient way to fit into a small area)	Students may think that this pattern doesn’t appear anywhere else. Students may not be able to find any pattern. If this is the case then have them look for a pattern of something small getting big and then section off the item to find a number for each group that is getting larger.
Evaluation(Decision Point Assessment)	The worksheets should be successfully completed.	Students should have the numbers in the Fibonacci sequence written next to each item on the worksheets.

Extend / Elaborate: Have students find the length and width of the following, and then find the ration of the length to width. a) a 3” x 5” index card b) an 8.5” x 11” paper c) a 2” x 3” school photo d) a familiar rectangle of their choice Approx. Time__15__mins	Write your measurements on the board (create a grid during the activity for them to fill in the answers), including item, length, width, and ratio (l/w). Do you see a pattern? What could we do to get one number from all of these ratios since they are close to each other? What is the average ratio?(1.61803) This is the Golden Ratio and it occurs in many pleasing shapes such as pentagons, crosses, and isosceles triangles. It’s often used in art and architecture. Can we relate the Fibonacci sequence and the Golden Ratio?	Students may not see the relationship between one object and another. Let the groups help these students and if they still can’t see it and ask them to observe the ratios and the closeness of one ratio to another. Students should be able to think of artifacts or structures in the world that might use the Golden Ratio. If they cannot think of structures that might include the Golden Ratio in their dimensions, then the teacher might need to bring in some pictures or make it a homework assignment.
Evaluation(Decision Point Assessment):	Look at the grid on the board for each group’s answers and determine the accuracy of each.	The students come up with the Golden Ratio and can find objects in the world in which the Golden Ratio is found.

Evaluate: Homework will be graded as well as classroom participation. Approx. Time__10__mins

Discuss the homework in the next class and ask about things that the students had trouble with in the homework after asking for questions that they might have.

Expect the students to say nothing was wrong, so look at the homework to figure out the areas that need work if this is the case.