Name:
Curt Wyman
Title of lesson: Two Dimensional Motion
Date of lesson: Fall, 2005
Second Six Weeks
Length of lesson: Two 75 Mins periods
Description of the class:
Grade
level: High School Physics
Sources for the lesson:
Holt Physics textbook, chap 3
AISG
Physics IPGÕs
Texas
Essential Knowledge and Skills for Science
TEKS addressed:
4. The student knows the laws governing motion.
The student is expected to be able
to:
(A)
generate and interpret graphs describing
motion including the use of real-time technology;
(B) analyze examples of uniform and
accelerated motion including linear, projectile, and circular;
(C) demonstrate the effects of forces on
the motion of objects;
Snapshot 4 (A)
¥ Generate and interpret
graphs of velocity/time, position/time.
Snapshot 4
(B)
¥ Design and illustrate an amusement park ride featuring
accelerated motion. Justify the safety and thrill components.
Snapshot 4
(C)
¥ Design and conduct demonstrations illustrating Newton's laws
of motion, such as rolling motion from roller blade wheels, pulling a
tablecloth out from under dishes on a table, and the stopping distance of a
car.
Snapshot 4
(D)
¥ Draw a free-body diagram for
an everyday situation such as the raising of a flag.
Identify the forces
present and describe their effects on the motion of the object.
Snapshot 4
(E)
¥
Describe and illustrate the motion of a
ball rolled across a merry-go-round from two frames of reference: on the
merry-go-round and off the merry-go-round.
The
Lesson: Two dimensional Motion Inquiry
I. Overview
In this lesson, students
will analytically investigate the motion of a roller coaster.
II. Performance or learner outcomes
The students
will be able to:
1. Describe the effects of the acceleration of gravity
on two dimensional motion.
2. Explain projectile motion.
3. Explain the effects of acceleration on initial and
final velocities.
4. Explain how a ramp affects the acceleration of
gravity and velocity calculations.
III. Resources, materials and supplies needed
1. Computer
Five E Organization – Day 1
Teacher
Does Student
Does
|
Engage: Time: 9:00 AM –
9:05 AM Hands out the work
sheet. Ask a volunteer sit in a
chair with a tennis ball and demonstrate JohnÕs position in the roller
coaster. Answer questions about
the problem and clarify the assumptions. |
Read the problem and ask
questions.
|
|
Explore: 9:05 – 9:45 AM Circulate among the groups and check on their progress. Answer questions without giving away any answers. |
Students work in teams
on the problem with their computers.
|
|
Explain: Time: 9:45 AM –
10:10 AM Ask several groups to
explain their solution one at at time. Have each team turn
in their solutions on USB drives or via email. |
The presenting group
will use the computer projector to show their work and explain their
solution. |
|
Extend/Elaborate: Introduce the second day
problem. |
|
Five E Organization – Day 2
Teacher
Does Student
Does
|
Engage: Time: 9:00 AM –
9:05 AM Hands out the work
sheet. Discuss briefly
differences from the day 1 problem. Answer questions about
the problem and clarify the assumptions. |
Read the problem and ask
questions.
|
|
Explore: 9:05 – 9:45 AM Circulate among the groups and check on their progress. Answer questions without giving away any answers. |
Students work in teams
on the problem with their computers.
|
|
Explain: Time: 9:45 AM –
10:10 AM Ask several groups to
explain their solution one at at time. Have each team turn
in their solutions on USB drives or via email. |
The presenting group
will use the computer projector to show their work and explain their
solution. |
|
Extend/Elaborate: Discuss the safety issues of actually performing this experiment on a real roller coaster. |
|
Lab Role:
_____________
Group #: _________
LAB TITILE: The Mysterious
Tennis Ball Experiment – Day 1
PURPOSE: To learn about the two dimensional motion, velocity
and acceleration
MATERIALS: Computer
INTRODUCTION: This is
an inquiry requiring you to solve
a problem involving a roller coaster and a tennis ball.
DIRECTIONS: Read the problem and perform an analysis to answer
the questions:
John has a tennis ball
attached to a 1.5 meter length of string.
He takes the ball and
string with him on a roller coaster.
He is riding in a seat by himself.
He ties one end of the string to his belt and at the top of the first
hill, holds the ball out one meter
in front of the empty seat beside him.
When the roller coaster starts down the nearly vertical hill, he
releases the ball and watches it.
What happens to JohnÕs
ball during the ride down the hill?
HereÕs the drawing for the
roller coaster.
Assumptions: The path of the first hill that we are
studying can be considered a straight line at an angle of 70û with the
horizontal. Likewise for the
second hill except itÕs angle is 60û.
We will also assume that
the roller coaster is frictionless and that the cart has enough protection so
that wind will not affect the tennis ball.
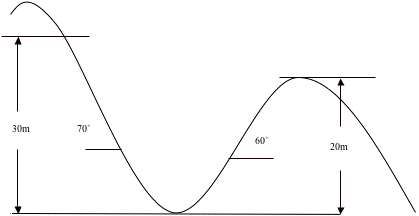
PART 1, Day 1: JohnÕs ride down hill
Qualitative analysis: Try to
visualize what will happen to the ball.
Discuss it
with your lab group. See if you can think of some simple experiments
that will lend insight to the problem.
Write down your hypothesis as to what will happen to the tennis ball.
Quantitative
Analysis: Define the calculations necessary to test your
hypothesis. Perform the
calculations and write up your conclusions with evidence.
Lab Role:
_____________
Group #: _________
LAB TITILE: The Mysterious
Tennis Ball Experiment - Day 2
PURPOSE: To learn about the two dimensional motion, velocity
and accelleration
MATERIALS: Computer
INTRODUCTION: This is
an inquiry requiring you to solve
a problem involving a roller coaster and a tennis ball.
DIRECTIONS: Read the problem and perform an analysis to answer
the questions:
Mary also has a tennis
ball and string with her on the same roller coaster. She ties the string to her belt and holds is out 1 meter in
front of the empty seat beside her and releases it at the bottom of the first
hill just as the roller coaster begins racing up the second hill.
What happens to MaryÕs
tennis ball during the ride up the hill?
HereÕs the drawing for the
roller coaster.
Assumptions: The path of the first hill that we are
studying can be considered a straight line at an angle of 70û with the
horizontal. Likewise for the
second hill except itÕs angle is 60û.
We will also assume that
the roller coaster is frictionless and that the cart has enough protection so
that wind will not affect the tennis ball.
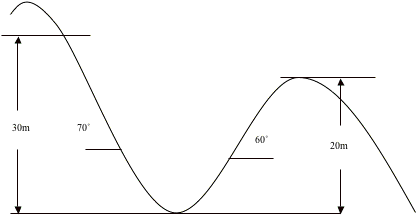
PART 2, Day 2: MaryÕs ride up the hill.
Qualitative
analysis: Like before, try to visualize what will happen to MaryÕs ball. Discuss it with your lab group. See if you can think of some simple
experiments that will lend insight to the problem. Write down your hypothesis as to what will happen to the
tennis ball.
Quantitative
Analysis: Define the calculations necessary to test your
hypothesis. Perform the
calculations and write up your conclusions with evidence.
2D Motion Solution
HereÕs the solution drawing for the roller coaster.
Assumptions: The path of the first hill that we are studying can be considered a straight line at an angle of 70û with the horizontal. Likewise for the second hill except itÕs angle is 60û.
We will also assume that the roller coaster is frictionless and that the cart has enough protection so that wind will not affect the tennis ball.
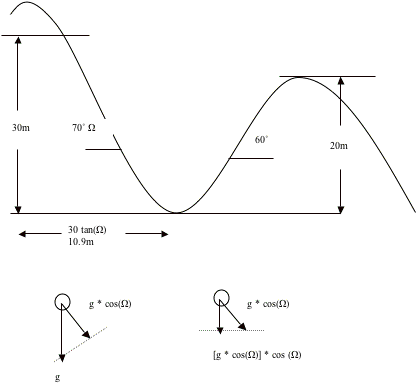
|
|
|
|
|
Notes |
|
|
|
|
|
|
|
|
|
Roller coaster car
numbers |
|
|
|
|
|
|
|
|
|
|
|
|
|
Height of 1st hill |
m |
30.0 |
|
|
|
|
1st hill track length |
m |
31.9 |
|
|
|
|
Horizontal distance to
bottom of hill |
m |
10.9 |
|
|
|
|
g |
m/s2 |
9.8 |
|
|
|
|
angle of slope, Ω |
deg |
20.0 |
0.349 |
rad |
|
|
g at the ramp angle |
m/s2 |
9.2 |
|
a |
|
|
g vertical component |
m/s2 |
8.7 |
|
b |
|
|
time to bottom of hill |
s |
2.6 |
|
c |
|
|
average velocity down
track |
m/s |
12.1 |
|
d |
|
|
Time to move 1 m
horizontally |
s |
0.8 |
|
|
|
|
Avg Vertical velocity |
m/s |
11.4 |
|
|
|
|
Avg horizontal velocity |
m/s |
4.1 |
|
|
|
|
Time to fall 5m |
s |
1.07 |
|
|
|
|
|
|
|
|
|
|
|
final velocity on track |
m/s |
24.2 |
e |
|
|
|
final vertical velocity |
m/s |
22.8 |
|
|
|
|
final horizontal
velocity |
m/s |
8.3 |
|
|
|
|
|
|
|
|
|
|
|
Tennis Ball numbers |
|
|
|
|
|
|
time to fall to the
ground |
s |
2.5 |
|
|
|
|
velocity avg |
m/s |
12.1 |
|
|
|
|
Time to fall 5m |
m |
1.01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Conclusion: The tennis ball falls only slightly
faster straight down than the roller coaster. To John, sitting next to it, the ball would appear to be
falling very slowly toward the bottom of the roller coaster car. However, the tennis ball is
moving to the back of the roller coaster fairly rapidly. John could watch as the ball moves
backwards and hits the empty seat.
This would take about a second or one third of the time of decent. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) g (slope) = g * cos(Ω) |
|
|
|
|
|
|
b) g vertical component
= g(slope) * cos(Ω) |
|
|
|||
|
c) time to bottom of
hill = Ã[(2 * track length) /(g slope)] |
|
||||
|
d) average velocity down
track = track length / time to bottom of hill |
|||||
|
e) final velocity = 2 *
avg velocity + initial velocity |
|
|
|||
|
initial vel = 0,
final vel = 2 *avg |
|
|
|
|
|