Name: Christopher Rodriguez

Title of Lesson: Sequences: Finding Patterns and Writing Explicit Formulas

Date of Lesson: Fall 2006

Length of Lesson: 50 minutes

Description of Class: Algebra II

Source of Lesson: http://uteach.utexas.edu/~gdickinson/pbi/PBIFall03/Fractal/content/Benchmark_Lesson_on_Sequenc.htm

TEKS addressed:

111.34. Geometry:

(G.1)(A)  develop an awareness of the structure of a mathematical system, connecting definitions, postulates, logical reasoning, and theorems;

(G.5)(A)  use numeric and geometric patterns to develop algebraic expressions representing geometric properties

Resources, materials and supplies needed – None

Supplementary materials, handouts – Worksheet: Explicit Sequences

Engage: `5 minutes
Teacher Does	Hoped for student response
Students will be presented these problems on the board: What are the next 3 numbers in these two patterns of numbers? 0, 5, 10, 15, . . . 2, 4, 8, 16, . . . After giving the students a few minutes to think about the problem, discuss with the class what the answers are.	First problem: 20, 25, 30 Second Problem: 32, 64, 128
Questions: What is the pattern you see with these two sets of numbers? How do you know what the pattern is? What is the difference to the two sets of numbers? Is the pattern different?	Expected Student Response: I expect that the students will be able to see what the pattern is.

Explore: 15 minutes
Teacher Does	Hoped for student response
Divide the students into groups of two or three. The groups are to come up with their own pattern for the class to solve. Give them each 5 minutes to come up with a set of numbers and be ready to share if called on. Instruct the students that the pattern must be visible within the first five numbers they present. Have two or three groups share their pattern with the class. Have the class solve the problems.	Students will design a pattern of numbers and be ready to share with the class. Groups will volunteer to share their problem (if not, call on random groups). The class will solve the problems (if not, have the group who presented the problem explain the solution).
Questions: What is going to make your pattern standout from everyone else’s? How will you prove that your solution is correct? Are there alternate solutions to your pattern?	Expected Student Response:

Explain: 10 minutes
Teacher Does	Hoped for student response:
After the students have shared their patterns, lead a class discussion of the difference between the two patterns that was looked at in the beginning of class. Explain to the students that the patterns are called sequences and explain the difference between an arithmetic sequence and a geometric sequence. An arithmetic sequence has a constant difference and a geometric sequence has a constant ratio. Then, work on writing the sequences out algebraically.	Students will listen and take notes.
Questions: What type of sequence did each of you create for your pattern? How do you know? Does your sequence have a beginning and an end?	Expected Student Response: Students will be able to answer each question.

Extend: 15 minutes
Teacher Does	Hoped for response:
Instruct the class that they will now complete a worksheet dealing with arithmetic and geometric sequences. Allow the students to remain in their groups. Ask for a volunteer to pass out the worksheet to the class. Monitor the groups to make sure there are no problems and that they are on task.	Students will stay on task and be able to complete the worksheet in the given time (if students have trouble, use the Questions given in the next pane)
Questions: How do we determine whether this sequence is arithmetic or geometric? Is there a constant difference or a constant ratio? Does your formula give you what you believe to be the next two or three terms?	Expected Student Response: Students will be able to answer the questions.

Evaluate: 5 minutes
Teacher Does	Hoped for response:
Have different groups present their solutions to the answers. Walk around the class to make sure other groups have the correct answer. Ask if any other groups received different answers and have them present their solution. Confirm what the correct answer is after the class has come to a consensus on what they feel to be the correct answer.	Students will agree on the correct answer (if not, have the students discuss why their different is correct)
Questions: Does anyone have a different answer? Did anyone do this problem differently? Which method is correct?	Expected Student Response: Students will present their different answers and methods. Students will agree on the correct method(s) to do the problem.

Name: _________________________________ Date: _____________

Worksheet: Explicit Sequences

For problems (1) and (2), on a separate sheet of paper, write out the sequences from the explicit formulas.

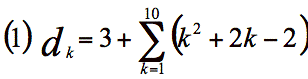
For problems (3) and (4), on a separate sheet of paper, find the explicit formula for the sequences.