Benchmark Lesson on Sequences

Engage: 10 minutes
Teacher Does	Hoped for student response
Have the students summarize the last two days of teaching (sequences, explicit and recursive). Then, tell how finding the formula to the sequence can be useful. If we know the formula for the sequence, then we can use the formula to give us any single term in the series. Ask the students for an example in the real world of when it could be useful to have a formula. Tell the students that the goal for today is to explore the different patterns that develop in our world.	Students will provide examples, population growth, interest rate or half-life decay.
*Questions:* What is a sequence? What types are there? Are there any famous ones? What patterns have we seen around us that we have given formulas?	*Expected Student Response*: Students will explain the differences between explicit and recursive sequences. Students will describe the Fibonacci sequence. Students will think of examples.
Teacher Does	Hoped for student response
Relate the discussion back to Fibonacci. Say that he was an Italian mathematician from the early 1200s. He was investigating how fast rabbits could breed under ideal circumstances. In developing the problem, he made the following assumptions: Begin with one male and one female rabbit. Rabbits can mate at the age of one month, so by the end of the second month, each female can produce another pair of rabbits. The rabbits never die. The female produces one male and one female every month. Fibonacci asked how many pairs of rabbits would be produced in one year. Tell the students that they will be trying to solve Fibonacci’s problem. Divide the students into groups of two or three. Remind them that they’re counting pairs of rabbits, not individual rabbits. Monitor the groups to make sure they are on task and that there are no problems. Tell the students it may be easier if they draw a family tree, beginning with the first pair. Once the groups have found how many rabbits are at the end of the first year, ask the students to give a formula to find the number of rabbits at the end of the second year.	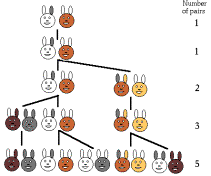Sample student tree diagram. Students will give the Fibonacci sequence.
*Questions*: How many pairs of rabbits do we have at the end of the first month? The second month? The third month? The fourth? How many months until a female rabbit can give birth? How many more rabbits does she give? What pattern is emerging? How can we represent this pattern?	*Expected Student Response:* At the end of the first month, there is one pair. 2 months = 2 pair; 3 months = 3 pairs; 4 months = 5 pairs . . . The rabbits mate at age one month, then produce a pair of offspring at the end of the second month, and mate again. By the end of the next month (3), another pair is produced. So at the start of fourth month, there are 3 pairs but two more pairs will be produced at the end of the month. The number of rabbits at the start of each month is 1, 1, 2, 3, 5, 8, 13, 21, 34, . . . The pattern can be represented with the Fibonacci sequence.

Explore: 20 minutes
Teacher Does	Hoped for student response:
Allow the students to remain in their groups. Tell the students that the Fibonacci numbers and sequence are everywhere in nature. Have a student volunteer to pass out the worksheet. Instruct the students to complete the worksheet and that they will discuss their answers towards the end of class.	Students will obey. Students will stay on task.
*Questions*: What do you notice about your answers? Do they have anything in common?	*Expected Student Response:* Students will recognize that all their answers were numbers from the Fibonacci sequence.

Explain: 10 minutes
Teacher Does	Hoped for response:
Have the groups discuss their answers. Have different students volunteer to show how they answered numbers two through five. Ask if other students came up with different methods and different answers. Make sure the discussion leads to the pictures dealing with the Fibonacci numbers.
*Questions:* How did you discover the spirals on the pictures? How many spirals were there? Why are these numbers important? Where did we see them before?	*Expected Student Response:* Students will answer that the numbers are Fibonacci numbers.

Extend: 10 minutes

Teacher Does

Hoped for response:

Refer back to the rabbit problem. Tell the students that their drawings were very nice. However, you found a virtual representation of the family tree. On a computer overhead, show this link: http://britton.disted.camosun.bc.ca/fibonacci/jbfibapplet.htm Play with the applet to show the students how the family tree evolves each month.

Tell the students that Fibonacci exists everywhere in nature, such as was seen earlier. The most common example from what was seen was the Fibonacci spiral. Although the amount of spirals was Fibonacci numbers, certain spirals come from the Fibonacci sequence. Show this link: http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html#spiral to display the applet involving building squares using the Fibonacci sequence. This rectangle is known as the Fibonacci Rectangle.

Show this link: http://nlvm.usu.edu/en/nav/frames_asid_133_g_3_t_3.html to show the spiral that can be formed inside the rectangle. Show pictures of different nautilus shells on the computer overhead projector.

Students will relate the virtual tree to their hand-drawn diagram.

Students will see the Fibonacci sequence in the Rectangle.

Evaluate
Teacher Does	Hoped for response:
The evaluation will be done during class by monitoring the groups to make sure they are on task and by evaluating the students during the discussion.