NAME: ____________________ DATE:
____________
Geometry in Nature
End of Unit Exam
For problems 1 – 3, write out the terms of the
sequences from the explicit formula. 5 points each
1.
![]()
2.
![]()
3.
![]()
For problems 4 – 6, find the explicit formula from the
given sequence. 5 points each
4.
4, 6, 13.5, 20.25, 30.375,
45.5625
5.
3, 5, 7, 9, 11, 13
6.
55, 89, 144, 233, 377, 610, 987
7.
If a shape “matches” itself only once in a full rotation, it
has rotational symmetry. 5
points
True / False (circle one).
8.
This shape is made up of five identical squares.
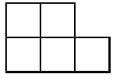
Draw one more square so that the new shape has exactly one line of symmetry.
Find two different ways to do it on the following
figures: 10 points

9.
Which of the
following letters of objects possess rotational symmetry? 5 points
(Circle ALL that apply)
(a) Letter F
(b) Equilateral triangle
(c) Letter X
(d) A rectangle
(e) A square
(f) Letter W
(g) Letter Q
10. In the figure shown below, consider the transformation that consists of a reflection through line m, followed by a rotation on 90° clockwise around point P.
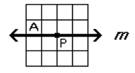
(a) Show the position of the
letter A shape under this transformation. (Draw it on the figure above making
sure I can tell what you intend your answer to be. 5 points
(b) Find a transformation or
sequence of transformations that undoes what this transformation did. In other words, what transformation
will send the A you drew back to the A in the original position. 5 points
11.
What are the properties of fractals? (Circle one) 5 points
(a) Self-symmetry
(b) Recursion
(c) Infiniteness
(d) Only a and c are correct.
(e) All of the above
12. The following table shows iteration results from the Sierpinski Triangle:
|
Stage |
# of Shaded
Triangles |
Number of
Unshaded Triangles |
|
0 |
1 |
0 |
|
1 |
3 |
1 |
|
2 |
9 |
4 |
|
3 |
27 |
13 |
|
4 |
81 |
40 |
(a) What is the n-th term formula
for shaded triangles? (Show your thought process) 5 points
(b) What is the n-th term formula for unshaded triangles? (Show your thought process)
5 points
13.
Determine which polygon the tessellation was made from by
connecting congruent points. 5
points

14.
Show that a 30°-60°-90° triangle is a rep-3 tile. 5 points
15.
Show that a right triangle whose legs measure 2 cm and 4 cm is
a rep-5 tile. 5 points
16.
One property of golden rectangles is that their ![]()
(a)
If we want to create a golden rectangle with width 9 cm, what
would the length be?
5 points
(b)
Draw this rectangle. 5 points
Total Score ______ / 100